| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 |
- professor strang
- ㅐㅕ세ㅕㅅ
- 선형대수학
- Gilbert Strang
- BAEKJOON
- adversarialattackonmonoculardepthestimation
- Algorithm
- CS231n
- 백준
- pycharmerror
- BOJ
- monoculardepthestimation
- 아이폰원스토어
- CNNarchitecture
- CS231nSVM
- CS231ntwolayerneuralnet
- CNN구조정리
- arm칩에안드로이드
- Linear algebra
- 맥실리콘
- 백준알고리즘
- 선대
- 맥북원스토어
- CS231nAssignments
- RegionProposalNetworks
- ios원스토어
- gpumemory
- MacOS
- CS231nAssignment1
- MIT
- Today
- Total
개발로 하는 개발
[CS231n] Assignment 1 - Softmax 본문
Softmax
Another popular classifier (like SVM)
Generalized version of binary Logistic Regression classifier
- Softmax function :

- Loss function : cross-entropy function

- Numerical Stability : exponential -> very large number -> normalize values

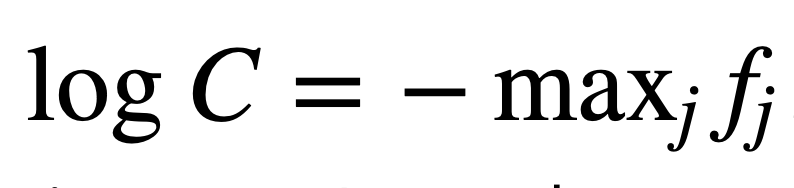
- SVM vs Softmax

Same score function Wx = b, different loss function.
Softmax : Calculate probabilities for each classes. Easier to interpret.
Softmax.py
1. def softmax_loss_naive(W, X, y, reg):
# compute the loss and the gradient
num_classes = W.shape[1] # 10
num_train = X.shape[0] # 500
loss = 0.0
for i in range(num_train):
scores = X[i].dot(W) # (10, ) = array of (sum of w * x)
# calculate the softmax loss of the class for ith training data and add it to loss
loss += - np.log(np.exp(scores[y[i]]) / np.sum(np.exp(scores)))
for j in range(num_classes):
dW[:,j] += X[i] * np.exp(scores[j]) / np.sum(np.exp(scores))
# - d (correct_class_score') / dW = - X[i]
dW[:,y[i]] -= X[i]
# Right now the loss is a sum over all training examples, but we want it
# to be an average instead so we divide by num_train.
loss /= num_train
dW /= num_train
# Add regularization to the loss.
loss += reg * np.sum(W * W)
dW += 2* reg * W # (reg * W * W)' = 2 * reg * W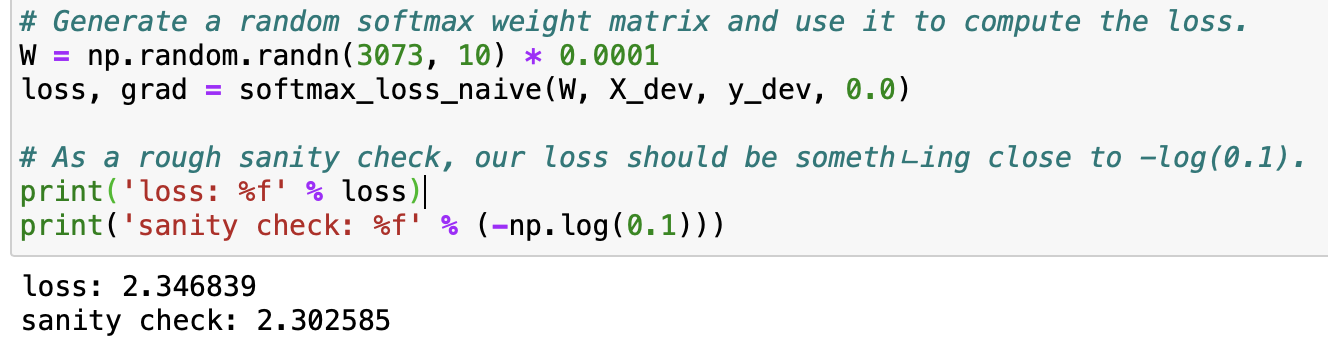
Because our dataset has 10 classes and the probability to selecting the right class when it is not trained is 1/10, the loss should be something close to -log(0.1).

2. def softmax_loss_vectorized(W, X, y, reg):
scores = X.dot(W)
# calculate the softmax loss
correct_scores = np.exp(scores[np.arange(X.shape[0]), y]) # (500, ), get the correct score x from x,y in scores
sum_exps = np.sum(np.exp(scores), axis = 1) # (500, )
loss = np.sum(-np.log(correct_scores/sum_exps))
#calculate the softmax gradient
#print(np.exp(scores).shape) # (500, 10)
#print(sum_exps.shape) # (500, )
mask = np.zeros_like(scores)
mask[np.arange(X.shape[0]), y] = -1;
mask += np.exp(scores) / sum_exps[:, np.newaxis]
dW += X.T.dot(mask)
#normalize
loss /= X.shape[0]
dW /= X.shape[0]
# Add regularization to the loss.
loss += reg * np.sum(W * W)
dW += 2* reg * W # (reg * W * W)' = 2 * reg * W
Hyperparameter tuning
# Provided as a reference. You may or may not want to change these hyperparameters
learning_rates = [1e-7, 5e-7]
regularization_strengths = [2.5e4, 5e4]
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
for lr in learning_rates:
for reg in regularization_strengths:
softmax = Softmax()
softmax.train(X_train, y_train, lr, reg, num_iters=1500, verbose=True)
y_train_pred = softmax.predict(X_train)
y_val_pred = softmax.predict(X_val)
results[(lr, reg)] = np.mean(y_train == y_train_pred), np.mean(y_val == y_val_pred)
if np.mean(y_val == y_val_pred) > best_val:
best_val = np.mean(y_val == y_val_pred)
best_softmax = softmax
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
# Print out results.
for lr, reg in sorted(results):
train_accuracy, val_accuracy = results[(lr, reg)]
print('lr %e reg %e train accuracy: %f val accuracy: %f' % (
lr, reg, train_accuracy, val_accuracy))
print('best validation accuracy achieved during cross-validation: %f' % best_val)
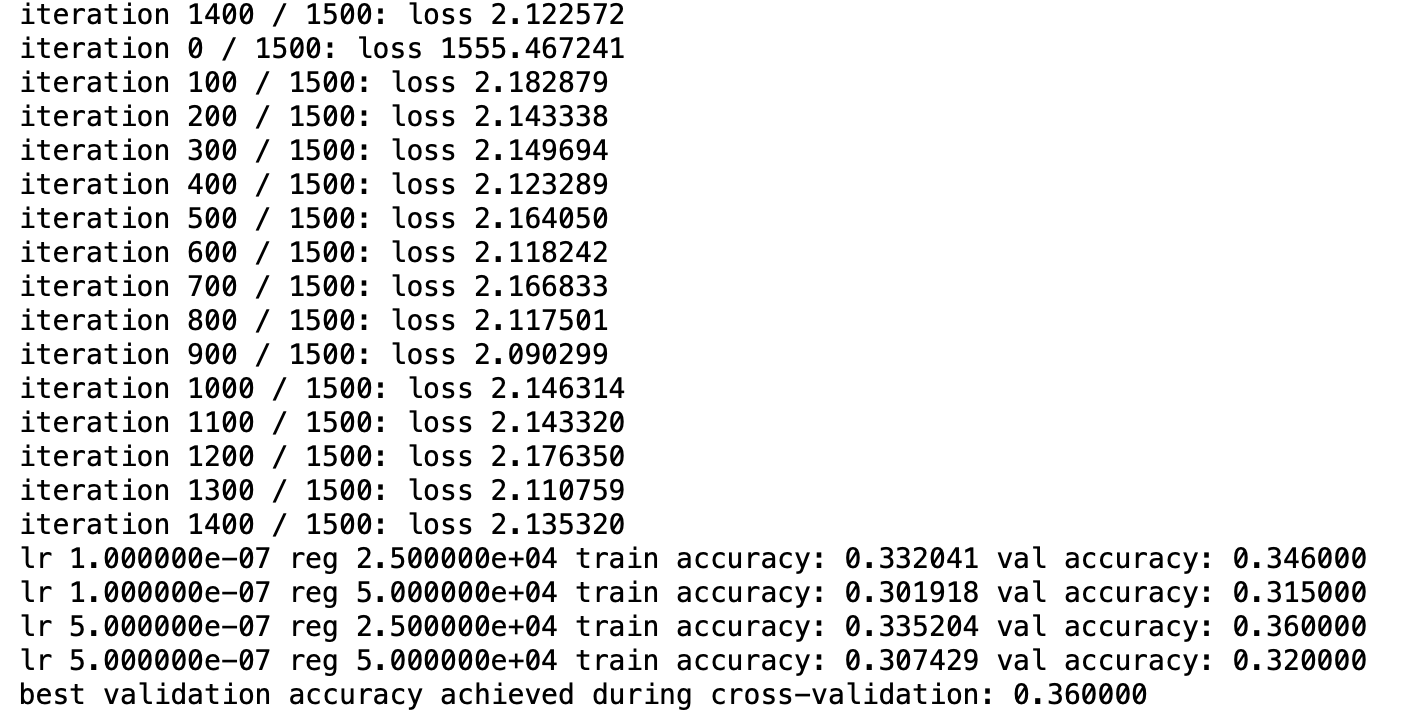
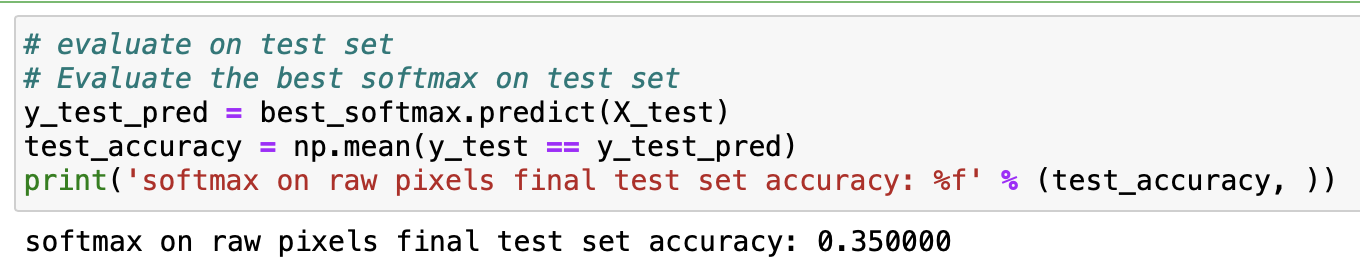
Results
1. test score
2. Visualize the learned weight

'Study' 카테고리의 다른 글
| [LG Aimers] Module 6. Deep Learning (1) | 2024.01.26 |
|---|---|
| [CS231n] Assignment 1 - Two Layer Net (0) | 2024.01.16 |
| [LG Aimers] Module 2. Mathematics for ML -1 (0) | 2024.01.13 |
| [LG Aimers] Module 1. 데이터의 분석과 AI 윤리 (0) | 2024.01.10 |
| [CS231n] Assignment 1 - SVM (0) | 2023.07.25 |



