| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
- adversarialattackonmonoculardepthestimation
- arm칩에안드로이드
- Algorithm
- CS231nAssignment1
- CNNarchitecture
- CS231nAssignments
- RegionProposalNetworks
- Gilbert Strang
- BOJ
- gpumemory
- CS231ntwolayerneuralnet
- 백준
- monoculardepthestimation
- pycharmerror
- MIT
- 맥실리콘
- Linear algebra
- CS231n
- 백준알고리즘
- 선형대수학
- 맥북원스토어
- CNN구조정리
- 아이폰원스토어
- ㅐㅕ세ㅕㅅ
- ios원스토어
- CS231nSVM
- MacOS
- 선대
- BAEKJOON
- professor strang
- Today
- Total
개발로 하는 개발
[LG Aimers] Module 6. Deep Learning 본문
1. Deep Neural Network (심층신경망)
- Perceptron
: Linear classifier $y = f(w_{0} + w_{1}x_{1} + w_{2}x_{2})$
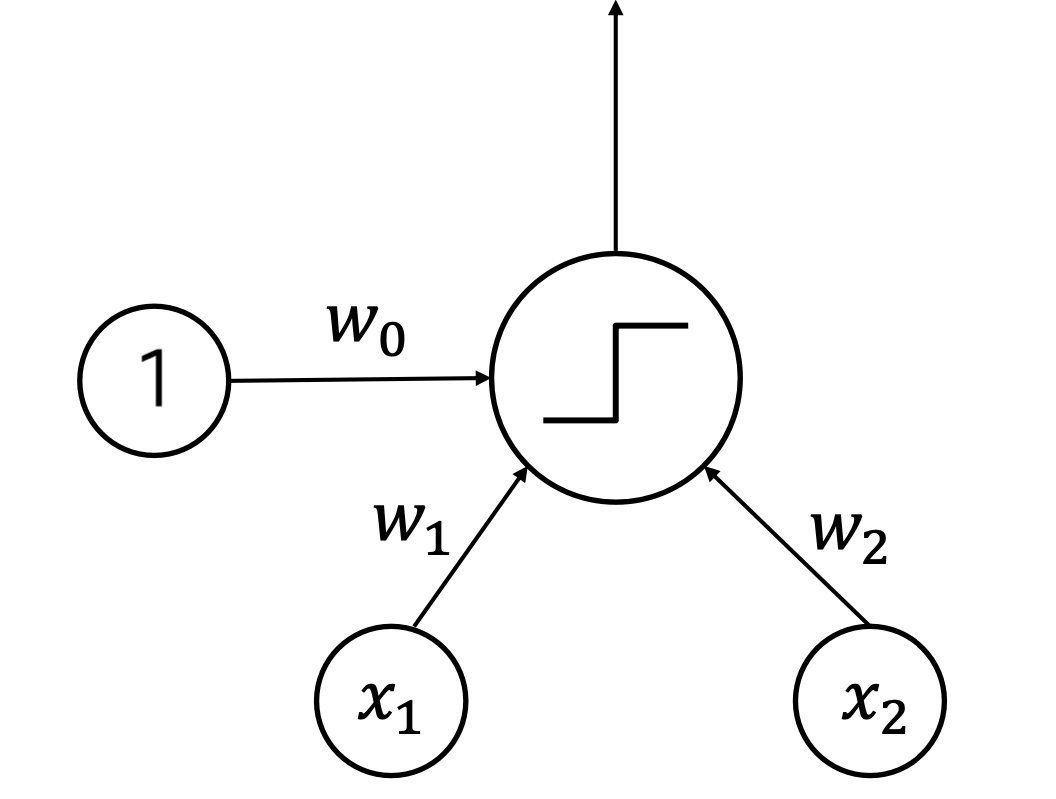
non-linear한 function을 계산하기 위해서는? multi-layer perceptron을 이용한다.
- hidden layer
: N-Layer Neural Network = (N-1)-hidden-layer Neural Network
- Forward Propagation
: Wx +b
2. Training Neural Networks
- Gradient Descent
: 일반적으로는 Adam이라는 방법이 최적
: local minima의 문제가 생길 수 있음
: ground truth 값에 대한 loss 값을 구하고, 편미분하여 gradient를 계산한다.
- Back Propagation
: 편미분 값을 계산해서 Gradient Descent algorithm의 parameter 최적화를 진행
: propagation 계산을 거꾸로 하는 것과 비슷해 보임
: 합성함수의 미분을 이용해서 계산
: output node의 gradient 값은 1.0에서 시작하여 역과정으로 수행된다.
- Sigmoid Function
: positive class에 대응하는 확률 값으로 해석
: $\sigma (x) = \frac{e^{x}}{e^{x}+1} = \frac{1}{1 + e^{-x}}$
: $\sigma(x) \leq \frac{1}{4}$, which decreases the gradient during backpropagation
: 여러 layer에 걸쳐서 sigmoid function이 있게 된다면, gradient vanishing problem이 발생
-> parameter update, converge가 느려짐
- Tanh Activation
: $tanh(x) = 2 \times sigmoid(x) - 1$
: range [-1, 1]
: zero-centered activation function
: 여전히 gradient 값이 여전히 0 ~ $\frac{1}{2}$ 사이라 gradient vanishing problem
- ReLU activation
: Rectified Linear Unit
: f(x) = max(0, x)
: does not saturate, computationally efficient
-> converge much faster than sigmoid/tanh
: not zero-centered output
: not differentiable
- Batch Normalization
: random gradients -> ReLU를 통하면 학습이 어려워짐
: activation function으로 입력되는 범위를 제한하는 방법 : batch normalization
: batch of activation -> normalization with values from batch
: batch normalization
: $\hat{x_{i}}^{k} = \frac{x_{i}^{k} - \mathbb{E}[x^{(k)}]}{\sqrt{Var[x^{(k)}]}}, y_{i}^{(k)} = \gamma^{(k)} \hat{x_{i}}^{k} + \beta^{(k)}$
: 이렇게 하면 그런데 기존의 분포를 무시하는 상황이라, 치명적인 영향을 줄 수도 있으므로 gradient descent를 통해 학습할 수 있는 $\gamma, \beta$를 통해 아래의 값을 가지면 고유의 분포를 따를 수 있게 해 준다.
: $\gamma^{(k)} = {\sqrt{Var[x^{(k)}]}}, \beta^{(k)} = \mathbb{E}[x^{(k)}$
'Study' 카테고리의 다른 글
| [Encoder - Decoder] Architecture (0) | 2024.02.27 |
|---|---|
| [CNN] architecture (0) | 2024.02.06 |
| [CS231n] Assignment 1 - Two Layer Net (0) | 2024.01.16 |
| [CS231n] Assignment 1 - Softmax (0) | 2024.01.16 |
| [LG Aimers] Module 2. Mathematics for ML -1 (0) | 2024.01.13 |



