Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 |
Tags
- 백준
- CS231nAssignments
- RegionProposalNetworks
- 아이폰원스토어
- BOJ
- pycharmerror
- adversarialattackonmonoculardepthestimation
- Algorithm
- CS231ntwolayerneuralnet
- gpumemory
- 백준알고리즘
- MacOS
- 맥북원스토어
- monoculardepthestimation
- 선대
- ㅐㅕ세ㅕㅅ
- CNNarchitecture
- CS231nSVM
- CS231n
- professor strang
- ios원스토어
- 선형대수학
- CNN구조정리
- Linear algebra
- 맥실리콘
- CS231nAssignment1
- Gilbert Strang
- MIT
- arm칩에안드로이드
- BAEKJOON
Archives
- Today
- Total
개발로 하는 개발
[CS231n] Assignment 1 - Two Layer Net 본문
Two Layer Net
biological neuron vs mathematical input&output of neuron
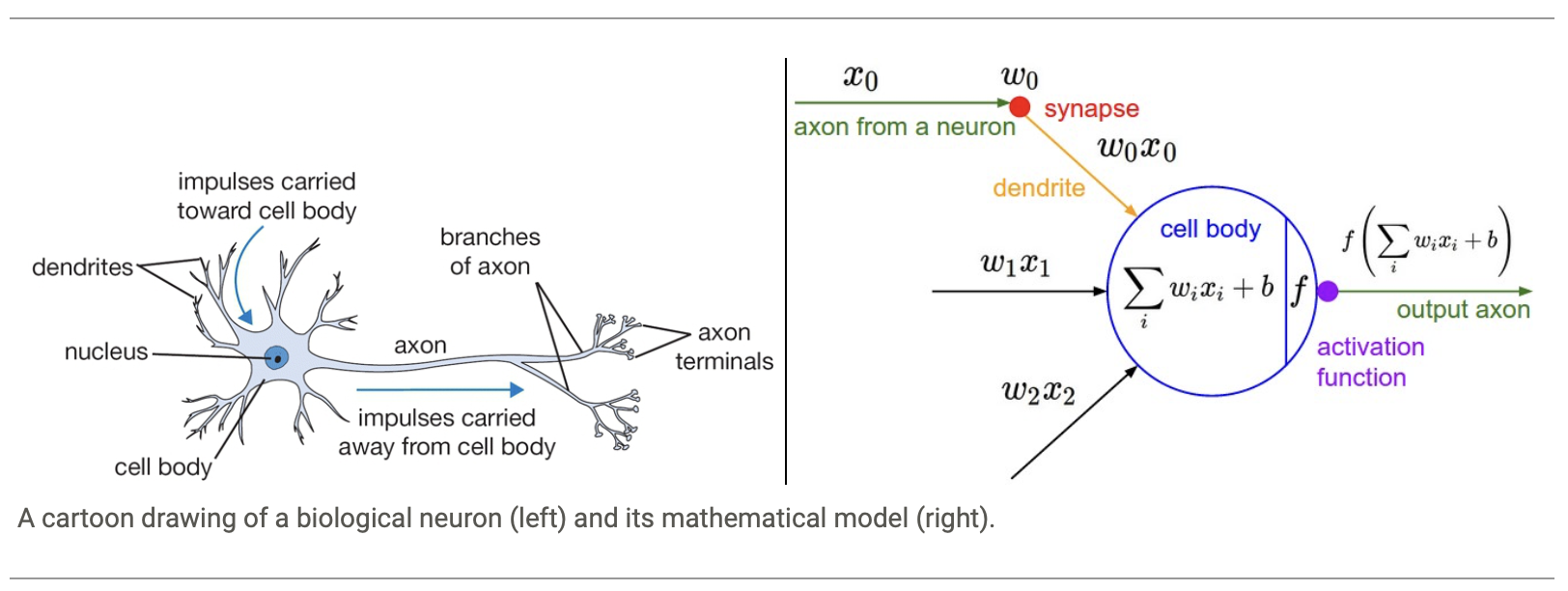
- activation function (or non-linearity)
takes a single number and performs a certain fixed mathematical operation on it






- fully-connected layer
in which neurons between two adjacent layers are fully pairwise connected, but neurons within a single layer share no connections

- Each Layer
usually matrix multiplication with activation function
# forward-pass of a 3-layer neural network:
f = lambda x: 1.0/(1.0 + np.exp(-x)) # activation function (use sigmoid)
x = np.random.randn(3, 1) # random input vector of three numbers (3x1)
h1 = f(np.dot(W1, x) + b1) # calculate first hidden layer activations (4x1)
h2 = f(np.dot(W2, h1) + b2) # calculate second hidden layer activations (4x1)
out = np.dot(W3, h2) + b3 # output neuron (1x1)
# where W1, W2, W3, b1, b2, b3 are learnable
Layers.py
1. def affine_forward(x, w, b):
#reshape x to (N, D)
reshaped_x = x.reshape(x.shape[0], -1)
out = np.dot(reshaped_x, w) + np.transpose(b)
2. def affine_backward(dout, cache):
# D = 6, M = 5, N = 10
dx = dout.dot(w.T).reshape(x.shape[0], *x.shape[1:]) # (N, M) * (D, M)^T -> (N, d_1, ... , d_k)
dw = x.reshape(x.shape[0], -1).T.dot(dout) # (N, D = {d_1, ..., d_k}) * (N, M) -> (D, M)
db = np.sum(dout, axis = 0) # (N, M) -> (M, )
3. def relu_forward(x)
out = np.maximum(0, x)
4. def relu_backward(dout, cache):
# for each cache > 0, dout * 1
mask = x > 0
dx = dout * mask
layer_utils.py
- implement using the methods in layer.py
1. def affine_relu_forward(x, w, b):
def affine_relu_forward(x, w, b):
"""
Convenience layer that perorms an affine transform followed by a ReLU
Inputs:
- x: Input to the affine layer
- w, b: Weights for the affine layer
Returns a tuple of:
- out: Output from the ReLU
- cache: Object to give to the backward pass
"""
a, fc_cache = affine_forward(x, w, b)
out, relu_cache = relu_forward(a)
cache = (fc_cache, relu_cache)
return out, cachedef affine_relu_backward(dout, cache):
"""
Backward pass for the affine-relu convenience layer
"""
fc_cache, relu_cache = cache
da = relu_backward(dout, relu_cache)
dx, dw, db = affine_backward(da, fc_cache)
return dx, dw, db
layers.py
1. def svm_loss(x, y):
num_train = x.shape[0] # N
correct_scores = x[np.arange(num_train), y] # (N, ), get the correct score from x
# note that for correct class, margin == 1
margins = np.maximum(0, x - correct_scores[:, np.newaxis] + 1) # (N, C)
# zero out the correct class
margins[np.arange(num_train), y] = 0
# normalize
loss = np.sum(margins) / num_train # (1, )
dx = (margins > 0).astype(float)
dx[range(num_train), y] -= dx.sum(axis=1)
dx /= num_train # normalize
2. def softmax_loss(x, y):
num_train = x.shape[0] # N
# calculate the softmax loss
correct_scores = np.exp(x[np.arange(num_train), y]) # (N, ), get the correct score from x
sum_exps = np.sum(np.exp(x), axis = 1) # (N, )
loss = - np.sum(np.log(correct_scores/sum_exps))
loss /= num_train #normalize
#calculate the softmax gradient
dx = np.zeros_like(x)
dx += np.exp(x) / sum_exps[:, np.newaxis]
dx[np.arange(num_train), y] -= 1
#normalize
dx /= num_train
fc_net.py
1. def __init__( self, input_dim=3 * 32 * 32, hidden_dim=100, num_classes=10, weight_scale=1e-3, reg=0.0):
self.params = {
'W1': np.random.randn(input_dim, hidden_dim) * weight_scale,
'b1': np.zeros(hidden_dim),
'W2': np.random.randn(hidden_dim, num_classes) * weight_scale,
'b2': np.zeros(num_classes)
}
2. def loss(self, X, y=None):
W1, b1, W2, b2 = self.params.values()
out1, cache = affine_relu_forward(X, W1, b1)
scores, cache3 = affine_forward(out1, W2, b2)loss, dloss = softmax_loss(scores, y)
loss += 0.5 * self.reg * (np.sum(W1**2) + np.sum(W2**2))
dx2, dw2, db2 = affine_backward(dloss, cache3)
dx1, dw1, db1 = affine_relu_backward(dx2, cache)
dw1 += self.reg * W1
dw2 += self.reg * W2
grads = {
'W1': dw1,
'b1': db1,
'W2': dw2,
'b2': db2
}
solver.py
solver = Solver(model, data, optim_config={'learning_rate': 1e-3})
solver.train()
Training Results


Hyperparameter Tuning
1. hyperparameter tuning
hidden_dims = [50, 100]
learning_rates = [1e-3, 1e-4]
epochs = [5, 10]
max_score = 0
reg_strengths = [10, 20]
for hd in hidden_dims:
for lr in learning_rates:
for e in epochs:
for rs in reg_strengths:
model = TwoLayerNet(hidden_dim = hd, reg = reg)
solver = Solver(model,data,optim_config = {'learning_rate': lr}, num_epochs = e, verbose = False)
solver.train()
accuracy = solver.check_accuracy(data['X_val'],data['y_val'])
if accuracy > max_score:
best_model = model
max_score = accuracy
print("with hidden_dims, learning_rates, epochs, reg_strengths = (", hd,", ", lr,",", e,",", rs, " ) accuracy : ",max_score)
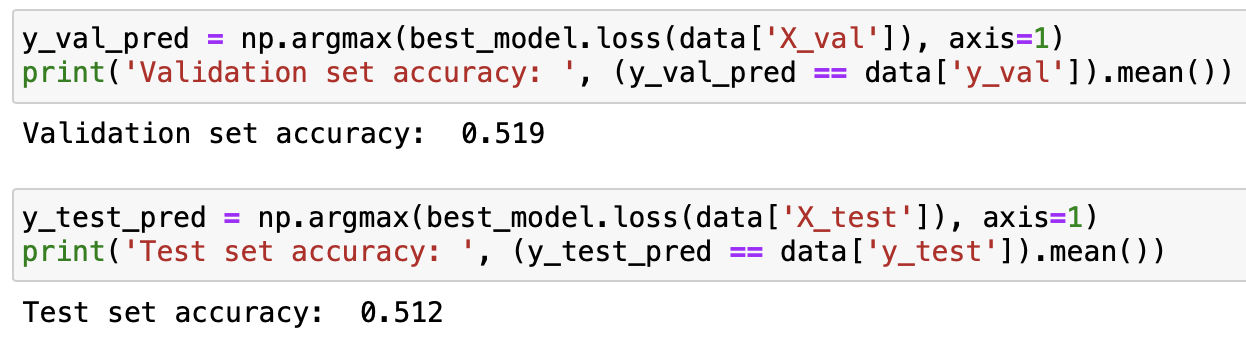
2. Validation, Test accuracy
'Study' 카테고리의 다른 글
| [CNN] architecture (0) | 2024.02.06 |
|---|---|
| [LG Aimers] Module 6. Deep Learning (1) | 2024.01.26 |
| [CS231n] Assignment 1 - Softmax (0) | 2024.01.16 |
| [LG Aimers] Module 2. Mathematics for ML -1 (0) | 2024.01.13 |
| [LG Aimers] Module 1. 데이터의 분석과 AI 윤리 (0) | 2024.01.10 |




